Any number can be expressed as the sum of powers of two.

For example, 21 = 16+4+1 = 2⁴+2²+2^0.

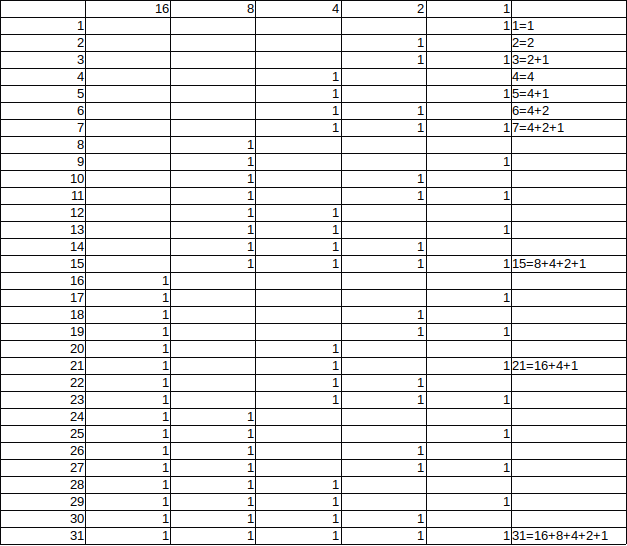
The cards have the numbers from 1 to 31. This table shows how each number can be expressed as the sum of powers of two. The table has one row for each of the numbers 1 to 31. It has one column for each of the powers of two that we need for the sums: 2⁴=16 ,2³=8 ,2²=4 ,2¹=2 ,2⁰=1.

Now we can place the numbers from 1 to 31 on the cards. All of the numbers that have 1 as part of the sum go on the ones card: 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31.

All of the numbers that have 2 as part of the sum go on the twos card: 2,3,6,7,10,11,14,15,18,19,22,23,26,27,30,31.

fours card: 4,5,6,7,12,13,14,15,20,21,22,23,28,29,30,31.

eights card: 8,9,10,11,12,13,14,15,24,25,26,27,28,29,30,31.

sixteens card: 16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31.

Then, when someone tells you which cards have their number all you have to do is add the first number on each of those cards.

If they say yes to the 16,4, and 1 card then you know they have 16+4+1=21.

This is the binary number system, which is how computers store numbers. In computer memory each of the columns in the table would be 1 bit of memory. With 4 bits of memory the largest value you can store is 16+8+4+2+1=31. Many modern computers use 64 bit memory which can store values up to 18,446,744,073,709,551,615 (2⁶³+2⁶²+2⁶¹+...+2^1).